论文分享：小样本 GNSS RAIM 漏检率评估：基于泊松分布的置信度控制方法

原文题目: GNSS receiver autonomous integrity monitoring missed detection evaluation method based on Poisson distribution

作者：李敏，李亮^*，李瑞杰，危亦林，蒋一平

来源: IEEE Transactions on Instrumentation and Measurement

论文引用:M. Li, L. Li, R. Li, Y. Wei and Y. Jiang, "GNSS receiver autonomous integrity monitoring missed detection evaluation method based on Poisson distribution," in IEEE Transactions on Instrumentation and Measurement, doi: 10.1109/TIM.2026.3659722.

原文链接：https://ieeexplore.ieee.org/document/11369295

一、主要贡献

• 提出了一种基于泊松分布的RAIM漏检率评估方法，可在小样本条件下同步约束I/II错误概率。相较于传统基于二项分布的评估方法，所提方法在满足评估置信度要求的同时显著降低了所需评估样本数；

• 采用泊松分布验后评估置信度模型对I/II类错误概率进行建模，并引入“死区”概念系统刻画两类错误概率与测试样本数、允许漏检样本数等评估参数间内在关联。针对不同初始样本数，依据“死区”制定的样本数调节策略可在两类错误受控前提下减少评估样本数量；

• 通过遍历全球用户位置、多种经典RAIM算法、典型漏检率评估样例的仿真与实测验证，系统地评估了方法的适用性与稳健性。结果表明，在合理采样周期下漏检样本服从泊松分布，此方法在小样本、严格置信度要求及不利用户位置条件下仍能提供可靠的漏检率评估，弥补了传统方法的局限。

二、研究背景

随着北斗与伽利略等多星座导航系统的快速发展，用户可获得的冗余观测显著增加，使基于接收机自主完整性监测（RAIM）的垂直引导进近（如LPV-200）在工程上具备可行性。为满足生命安全类应用对完整性和可靠性的严格要求，亟需建立更加严谨且可验证的RAIM完好性测试与性能评估方法。

在RAIM完好性测试中漏检率（PMD）评估是关键环节。现有PMD评估方法主要包括穷举测试法和解析法。穷举测试不依赖先验分布假设，但在评估 LPV-200等严苛PMD指标时所需测试周期极长，工程实现成本过高。解析法通常基于高斯误差假设，通过最差故障条件下的蒙特卡洛仿真加速评估过程，但其评估置信度易受电离层、多路径等非高斯误差影响。为规避先验误差分布假设，基于二项分布的假设检验方法通过I/II类错误概率刻画评估置信度，虽可显著降低样本需求，但在小样本和高完好要求条件下难以同时约束两类错误概率，尤其在LPV-200等高完好应用场景中暴露出明显局限。

三、算法框架

基于泊松分布的PMD评估方法同步控制两类错误的策略如图1所示。该方法以给定的初始测试样本数为约束，并结合漏检性能合格/不合格（分别对应H₀/H₁）典型值下的评估置信度需求，调整所需测试样本数和对应的允许漏检样本数（即测试门限），从而实现控制两类错误且最大程度减少所需测试样本的设计目标。首先引入死区系数以确定使测试样本数最小的测试门限，并据此计算对应的候选样本数集合以及。随后，根据初始测试样本数在该集合中的归属关系，将调整过程划分为三种情形，并分别制定相应的参数调整策略。在情形1和2下均可调整至理想的最小测试样本数以满足评估置信度；而在情形3下，为实现两类错误的同步控制，则需通过增加测试样本数或适当放宽H₁下的PMD约束。

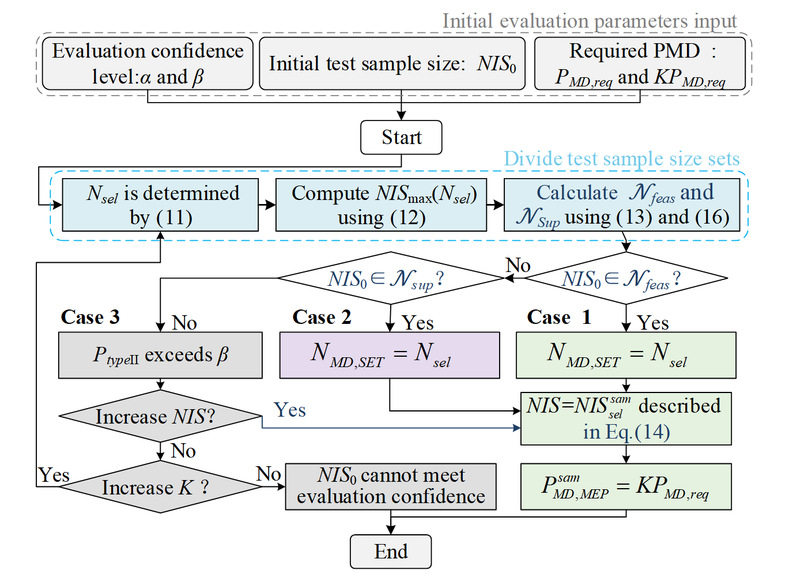
图1所提方法评估参数调整策略流程图

四、实验验证

为验证所提方法评估能力，选取两种主流评估方法作为对照，针对PMD评估选取特定三组参数案例，分析评估置信度与评估效率。三种方法具体如下：

经验法：收集测试时间段内所有样本，比较漏检样本数与总测试样本数比值与所需PMD判定RAIM算法是否满足完好性需求；

二项法：基于漏检样本数服从二项分布构建评估置信度模型，基于精确漏检率置信区间调整所需测试样本数与相应测试门限，比较漏检样本数与测试门限判定RAIM算法是否满足漏检率需求；

所提方法：与二项法类似，但基于泊松分布构建评估置信度模型，改进评估参数的调整策略。

(1)所提方法优势分析

在预设的三组初始样本下，采用所提方法获取评估参数对应表1的I/II类错误概率均低于指标α/β，具备显著的两类错误同步控制优势，并且由于精准的参数调整策略，最小可评估漏检率(P MD,MEP)最接近H₁下的预设指标K，所需样本数相比经验法与二项法至多可降低22.98%与63.40%。图2展示了在三类方法中，所提方法对PMD置信区间（PCI）的估计误差最小，同步约束I/II类错误概率能力更强。

表1三种方法评估能力对比(α=β=5%)

注：H₀：RAIM算法实际漏检率P MD,ref不高于漏检率需求PMD,req，H₁：P MD,ref高于PMD,req。

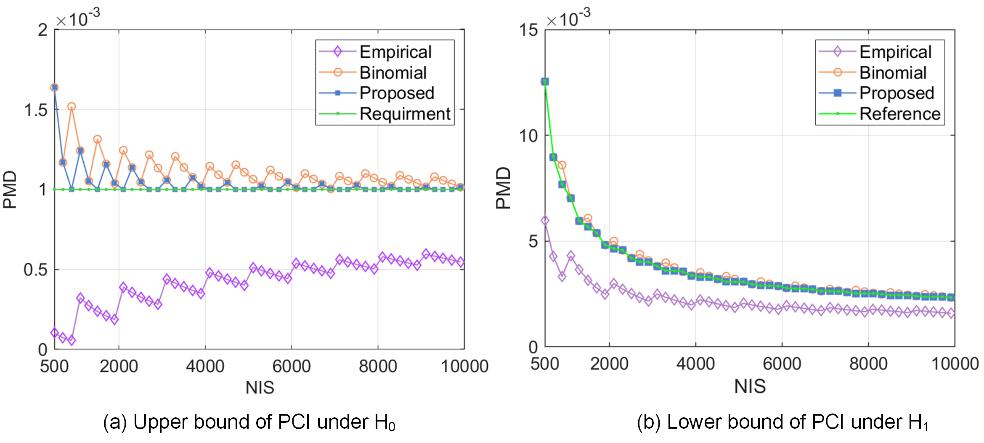
图2H₀/H₁下三类方法PMD置信区间（PCI）一致性比较：各类方法计算得到的PCI边界与需求（H₀）/基准参考（H₁）线的重合程度决定了对I/II类错误的控制能力，重合程度越高，控制能力越强。

(2)仿真环境多场景验证

从测试多种经典RAIM算法、设置三组典型评估样例、遍历全球用户位置等角度，对比三类方法的评估成功率（ESR）充分验证了所提方法可使用最少的样本数，以评估置信度不低于α/β的评估能力验证RAIM算法性能是否满足完好性能需求。

在北京测试点位上，对解分离法（SS-RAIM）、残差卡方法RAIM（RB-RAIM）、奇偶矢量法（PS-RAIM）等三种典型的RAIM算法测试，获得结果如图3/图4所示。对照表1可知，图3表明经验法出现II类错误事件，二项法与所提方法均可正确评估算法漏检性能，且所提方法所需样本最少。图4中所提方法ESR均不低于95%的评估置信度，而经验法仅H₁下满足评估置信度要求，二项法对ESR的控制较为均衡，但也未能同时满足H₀/H₁置信度要求。所提方法在评估置信度上的显著优势来源于如图5所示的泊松分布模型对两类错误概率的精准刻画。

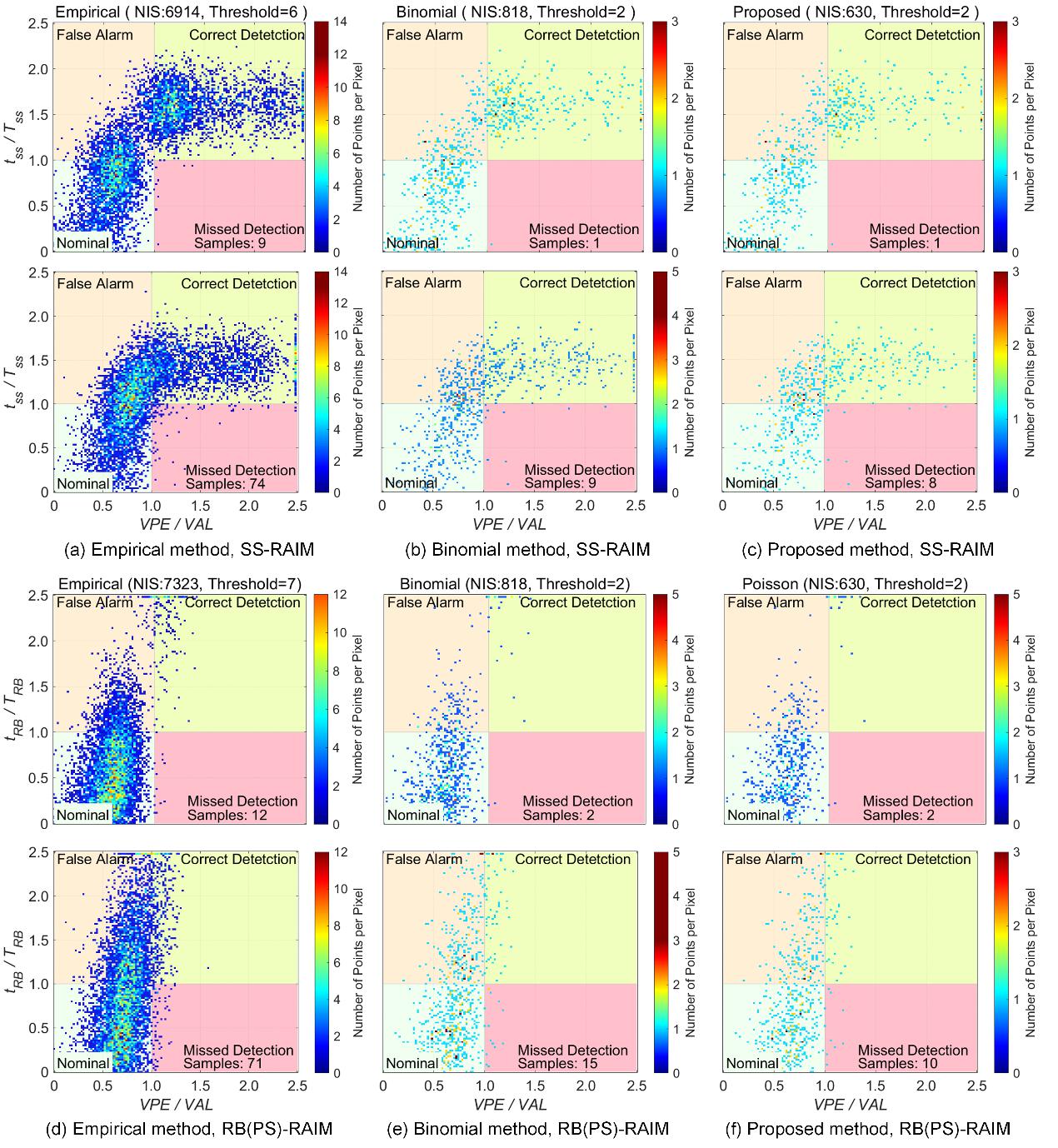
图3三类方法单次评估结果，H₀：PMD = 10⁻³（a/b/c），H₁：PMD = 10⁻²（d/e/f）。

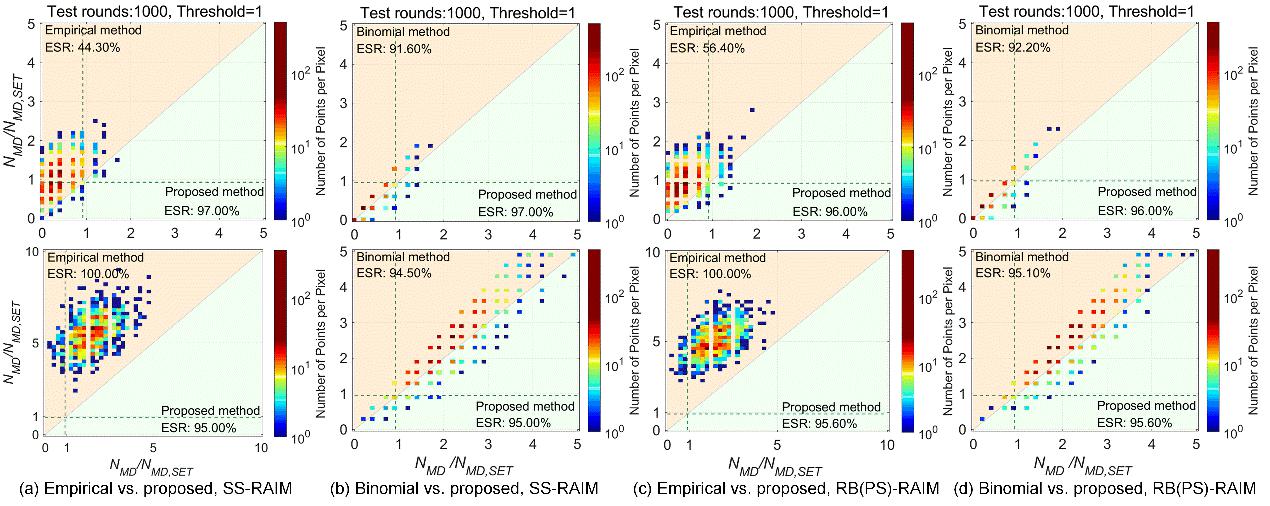
图4三类方法评估成功率，H₀：PMD = 10⁻³（a/b），H₁：PMD = 5×10⁻³（c/d）。

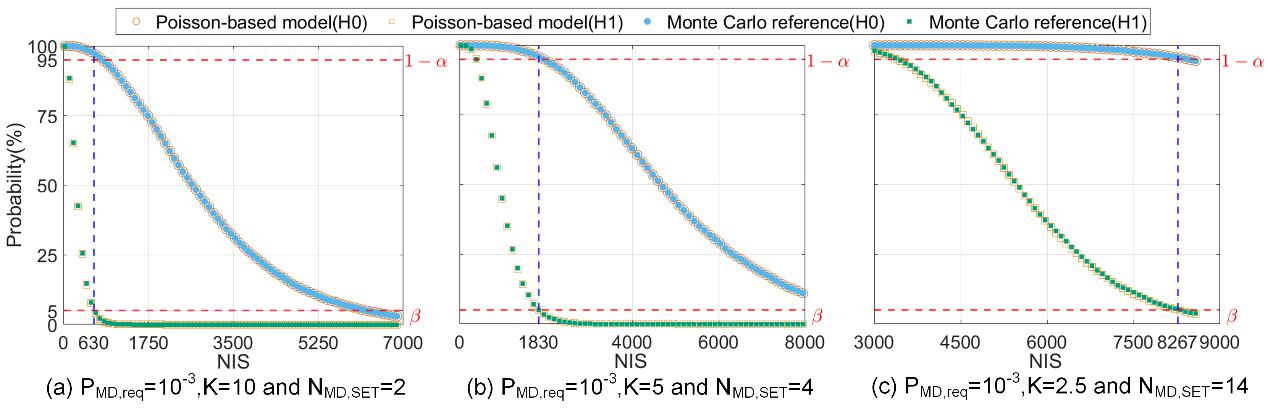
图5三组典型评估样例下，基于泊松分布的概率模型与蒙特卡洛仿真结果对比。结果表明，该模型能够准确刻画评估置信度，并给出同步约束第一类与第二类错误概率所需的测试样本数（蓝色虚线）。

选取全球均匀分布的20个测试点位（图6），分析所提方法在全球范围内的适用性。实验结果充分表明该方法在不同样本数和测试地点下均具有更高的稳定性与工程适用价值：

在初始测试样本充足的条件下，所提方法在所有用户位置和假设条件下均满足95%以上的评估置信度，实现了两类错误的同步可控，同时显著降低了所需测试样本数量。相比之下，传统经验法和二项分布法均无法在所有场景下兼顾两类错误控制，评估可靠性存在明显不足。

在初始样本数受限的挑战性条件下（阴影部分），所提方法依然展现出明显优势。即便在个别不利用户位置无法完全达到目标置信度，其整体评估置信度仍优于现有方法，并通过评估参数调整优先保障I类错误受控、最大限度降低II类错误概率。

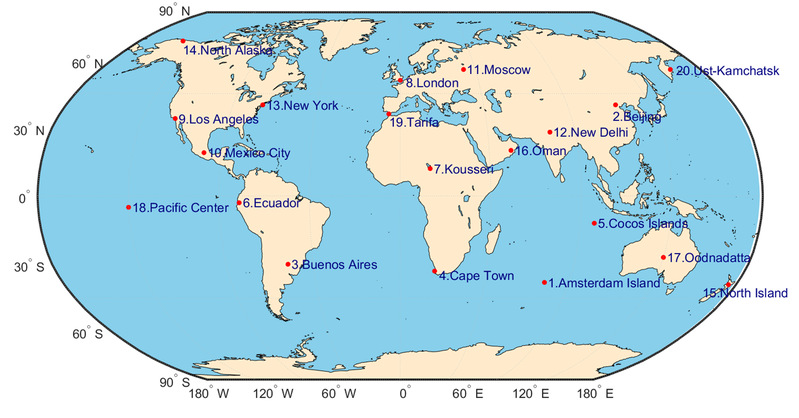
图6全球分布的20个测试点位。

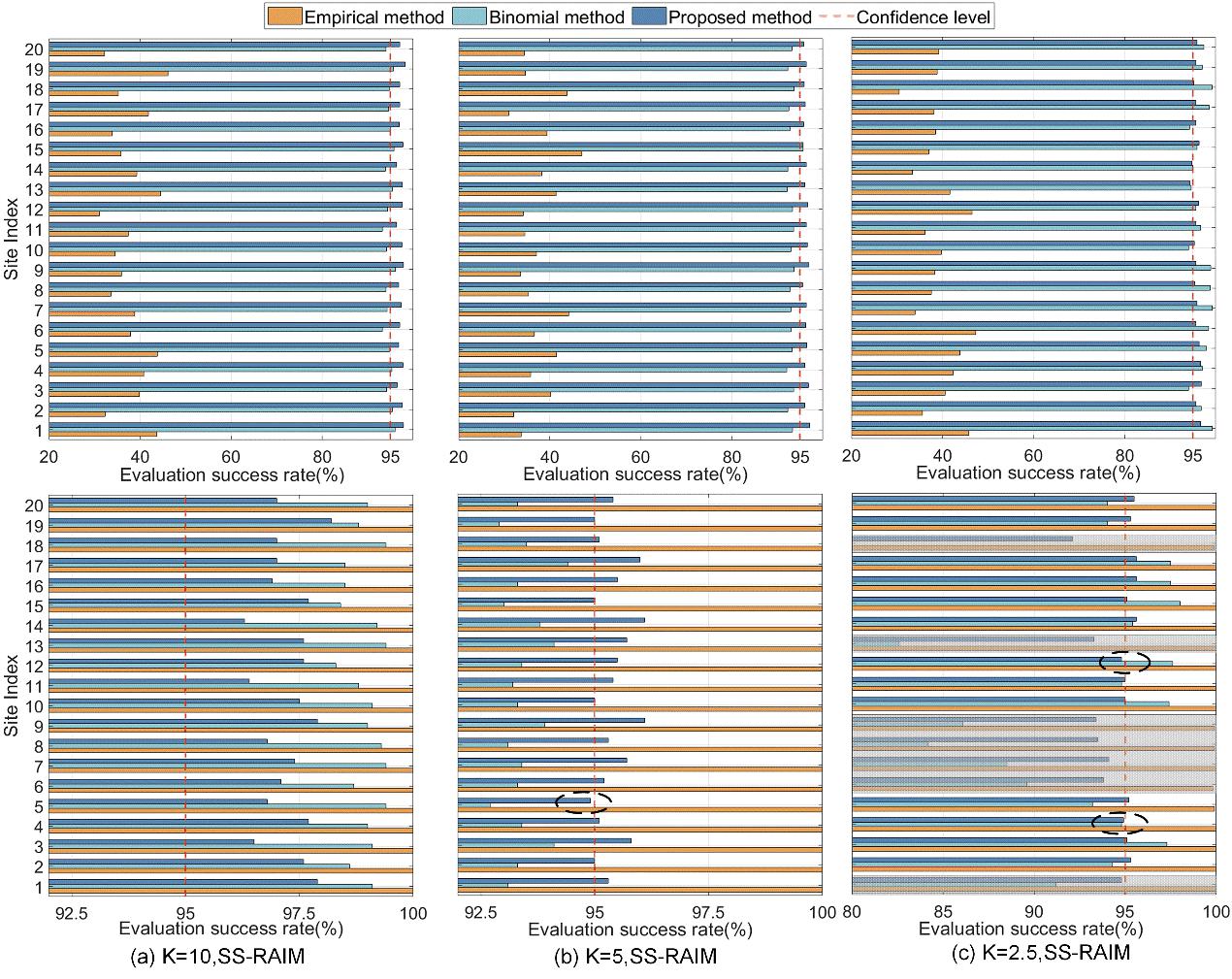
图720个测试点位评估成功率分布：灰色阴影表示情形3（样本数不足）对应的测试地点，黑色圈线标出所提方法在个别点位下未满足评估置信度要求的情况。

采用典型的一阶高斯–马尔科夫（FOGM）模型刻画实际测试样本之间的时间相关性。图8的结果显示，采样周期短于10 s时样本相关性显著增强，进而严重削弱评估置信度；随着采样周期增大至60s，样本相关性逐渐减弱，ESR明显提升并逐步逼近基于泊松分布模型计算的理论评估置信度。结果表明，通过合理选择采样周期，可有效缓解样本相关性对评估置信度的不利影响。

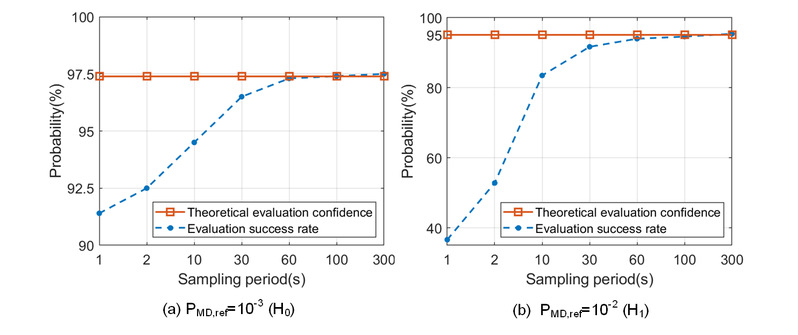
图8FOGM量测误差下不同采样周期对应的ESR。

（3）实际数据验证

根据仿真结论采用60 s采样周期以保证样本独立性。引入bootstrap方法对采集自五个实际测站的10天实测数据生成10,000组等效测试样本验证泊松分布模型的有效性。图9表明泊松分布均能较好刻画三组典型漏检样本数的经验分布，其参数估计结果与理论预期一致，验证了在真实数据条件下采用泊松分布建模漏检样本数的合理性。

图9H₀/H₁条件下基于实际数据的泊松分布拟合优度分析

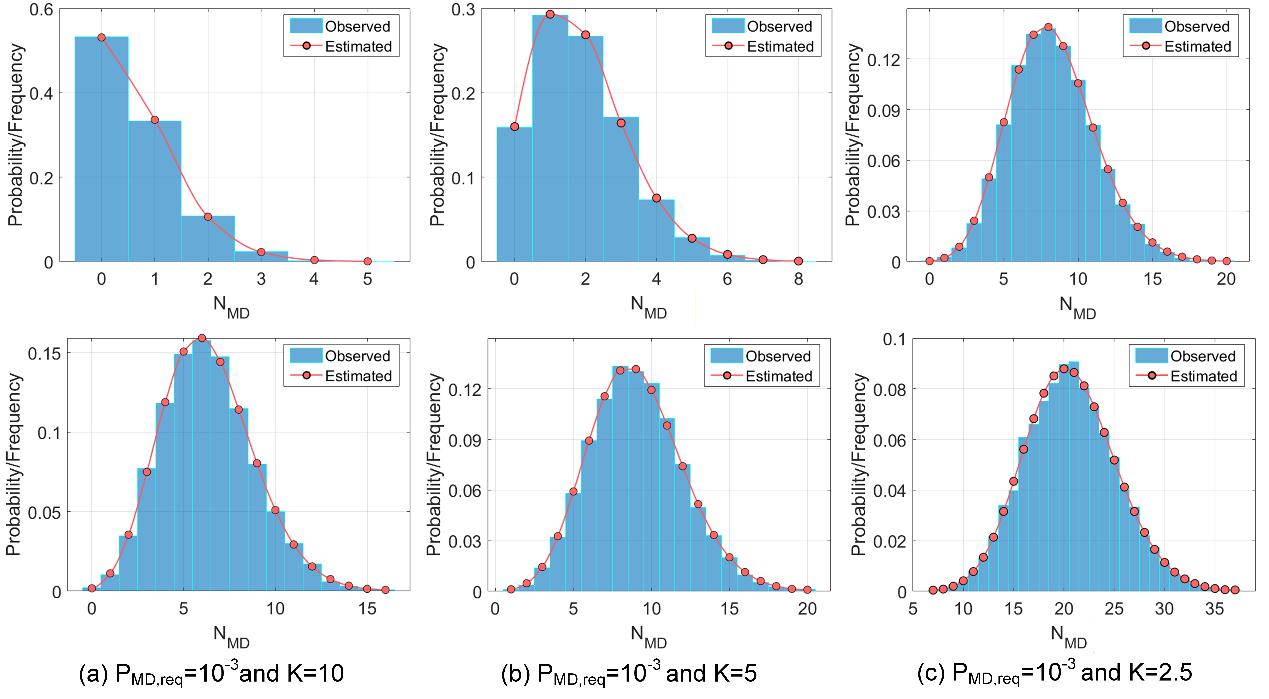
在三组典型评估案例下，表2表明提高采样频率虽然显著增加了测试样本数量，但破坏了样本独立性假设，所提方法与二项分布法的评估结果均受到一定影响。尽管如此，所提方法得益于更高的置信裕度，在K=5和K=2.5案例中仍能获得正确可靠的评估结果。二项法在更为严格的评估要求下（如K=2.5），所需测试样本数较所提方法多，不足以满足所需评估置信度；在卫星几何条件较优的用户位置（如DLF1和JPLM）下，漏检样本出现频率较低导致初始样本数减少，难以控制II类错误概率。

表260秒采样周期周期下PMD评估结果

综合多测站实际数据评估结果（图10）表明，样本相关性显著影响PMD评估置信度。在短采样周期条件下，ESR难以达到理论置信度，且该偏差在H₁条件下更为明显。随着采样周期增至60 s，样本相关性显著减弱，评估结果在各测站上整体逼近理论置信度水平。结果同时表明，良好的卫星几何条件如DLF1、JPLM在可在一定程度上缓解样本相关性对评估置信度的不利影响。在实际应用中足够长的采样周期对保障PMD评估置信度是必要的。

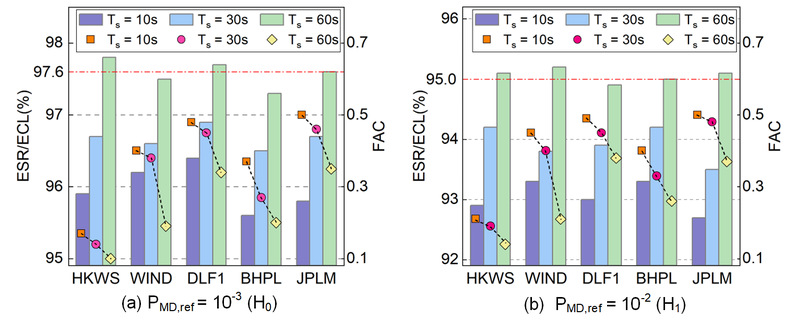
图10不同采样周期下实际数据下所提方法置信水平及其相关性

五、总结

所提方法为RAIM算法漏检性能评估提供了一种统计严谨且高效可行的解决方案，可同步控制两类错误并显著降低实验成本。该方法在多种RAIM算法及全球用户位置下均表现出良好的适用性，为漏检性能评估提供了实用框架。同时建议在应用此方法前开展泊松拟合优度检验与样本时间相关性分析。该方法有望为现有RAIM及未来ARAIM用户算法设备的完整性风险评估提供有力支撑。

团队介绍

卫星联合增强导航技术团队隶属于哈尔滨工程大学智能科学与工程学院，面向国家海洋强国战略，开展卫星导航高精度定位完好性监测的应用基础研究，研制多型海洋高精度北斗导航增强系统装备，并在国家多个海洋重点型号平台上得到批量业务化应用。

李亮，哈尔滨工程大学教授，博士生导师。长期在卫星导航高精度定位完好性监测方向开展研究工作，入选国家高层次青年人才计划，获得黑龙江省优秀青年基金资助。担任国际大地测量协会协同定位完好性监测工作组主席，工信部重点实验室常务副主任。作为项目责任人承担国家自然科学基金、国家重点研发计划课题、工信部高技术船、军种预研、型号科研等多个项目，主持研制多个导航系统型号装备。在国内外导航顶级期刊、顶级会议发表SCI论文40余篇。以第一发明人授权发明专利20余项，转让第一发明人的发明专利4项。曾获国防科技进步一等奖、中国海洋科学技术进步二等奖等8项省部级奖励。

李敏（第一作者），哈尔滨工程大学智能科学与工程学院博士研究生。主要研究内容包括高精度GNSS完好性监测、测试及评估等。